 S. Let xibe a strategy profile of player i and x-i be a strategy profile of all players except for player i. When each player i
S. Let xibe a strategy profile of player i and x-i be a strategy profile of all players except for player i. When each player i  {1, ..., n} chooses strategy xi resulting in strategy profile x = (x1, ..., xn)then player i obtains payoff fi(x). Note that the payoff depends on the strategy profile chosen, i.e., on the strategy chosen by player i as well as the strategies chosen by all the other players. A strategy profile x*
{1, ..., n} chooses strategy xi resulting in strategy profile x = (x1, ..., xn)then player i obtains payoff fi(x). Note that the payoff depends on the strategy profile chosen, i.e., on the strategy chosen by player i as well as the strategies chosen by all the other players. A strategy profile x*  S is a Nash equilibrium (NE) if no unilateral deviation in strategy by any single player is profitable for that player, that is
S is a Nash equilibrium (NE) if no unilateral deviation in strategy by any single player is profitable for that player, that isA game can have either a pure-strategy or a mixed Nash Equilibrium, (in the latter a pure strategy is chosen stochastically with a fixed frequency). Nash proved that if we allow mixed strategies, then every game with a finite number of players in which each player can choose from finitely many pure strategies has at least one Nash equilibrium.
When the inequality above holds strictly (with > instead of  ) for all players and all feasible alternative strategies, then the equilibrium is classified as a strict Nash equilibrium. If instead, for some player, there is exact equality between
) for all players and all feasible alternative strategies, then the equilibrium is classified as a strict Nash equilibrium. If instead, for some player, there is exact equality between  and some other strategy in the set S, then the equilibrium is classified as a weak Nash equilibrium.
and some other strategy in the set S, then the equilibrium is classified as a weak Nash equilibrium.

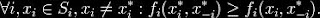
No comments:
Post a Comment